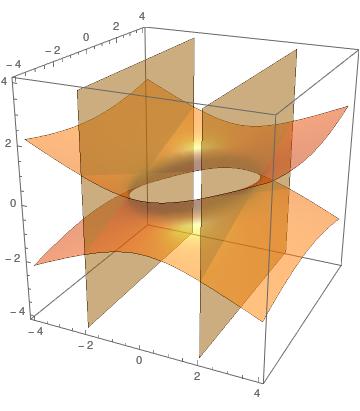
Trace the surface x^2/4+y^2/9-z^2/4=1. Also, describe its sections by the planes x=±2,algebraically and geometrically.? | Socratic
Graph △XYZ with vertices X(2, 3), Y(−3, 2), and Z(−4,−3) and its image after the translation (x, y)→(x+3, - Brainly.com
multivariable calculus - Volume of region bounded by $z=4 - \sqrt{x^2 +y^2}$ and $z=\sqrt{ x^2 +y^2}$ - Mathematics Stack Exchange
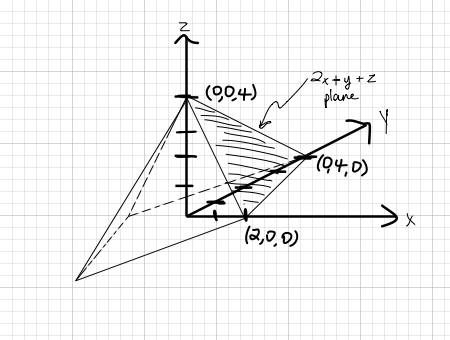
The tetrahedron enclosed by the coordinates planes and the plane 2x+y+z=4, how do you find the volume? | Socratic
Quadric Surfaces
Solved Find the volume of the solid bounded by the plane z = | Chegg.com
If `x : y = 2 : 3 , y : z = 4 : 7 `, then find `x : y : z`. - YouTube
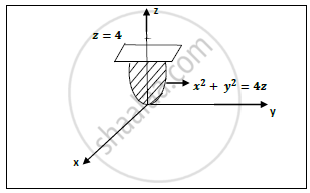
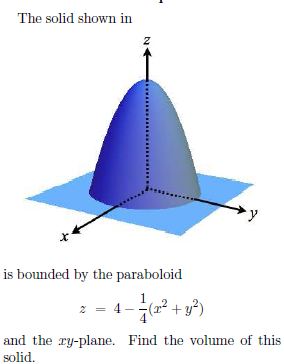
Find the Volume of the Paraboloid X 2 + Y 2 = 4 Z Cut off by the Plane 𝒛=𝟒 - Applied Mathematics 2 | Shaalaa.com
Surfaces, Part 2
If 2^x = 4^y = 8^z and xyz = 288, then find the value of x + y + z
Misc 16 - Solve equations 2/x +3/y +10/z = 4 4/x + 6/y +5/z = 1
se11f01_01.gif
calculus - Evaluating stokes theorem $\int \vec{F} \cdot d\vec{r}$ on the surface $z=4-y^2$ - Mathematics Stack Exchange
Q2If x 2 y 3 and z 4 find the value of ...
Solved Match each function with its graph. z = (4x2 + | Chegg.com
Is there a more romantic equation?! ❤️ : r/mathmemes
Quadric Surfaces
Find the volume of the bounded by the cylinder x^2+y^2=4 & the planes y+z=4, z=0 - YouTube
What is the surface area of the portion of the paraboloid z = 4 - 𝑥^2 -𝑦^2 that lies above the xy- plane? - Quora
![Prove that |[x,x^(2),x^(4)],[y,y^(2),y^(4)],[z,z^(2),z^(4 )]|=xyz(x-y)(y-z)(z-x)(x+y+z)](https://d10lpgp6xz60nq.cloudfront.net/web-thumb/244020970_web.png "Prove that |[x,x^(2),x^(4)],[y,y^(2),y^(4)],[z,z^(2),z^(4 )]|=xyz(x-y)(y-z)(z-x)(x+y+z)")
Prove that |[x,x^(2),x^(4)],[y,y^(2),y^(4)],[z,z^(2),z^(4 )]|=xyz(x-y)(y-z)(z-x)(x+y+z)
plotting - Traces of the level surface $z=4x^2+y^2$ - Mathematica Stack Exchange
Show that the lines x - 1/2 = y - 2/3 = z - 3/4 and x - 4/5 = y - 1/2 = z intersect. Also, find their point of intersection. - Sarthaks eConnect | Largest Online Education Community
Cylindrical Surfaces
Let 2x+3y+4z = 9, x,y,z > 0 then find the maximum value of (1+x)^2 (2+y)^3(4 +z)^4
Surface Area
Solved z = 4 - y^2 in a 3D graph | Chegg.com
